차량동역학 [1/4차량모델 (Quarter-Car Model)]

이 단원에서는 첫번째로 자동차의 진동, 안락함 등을 진동 모델을 알아보고, 차량의 1/4모델을 동역학적으로 유도해보겠습니다. 자동차에서 진동은 여러 원인에 의해 생겨납니다. 예를 들어, 엔진 진동, 브레이크와 클러치의 마찰 진동, 울퉁불퉁한 노면과 고르지 않는 타이어의 경우가 있습니다.

위 표는 자동차에 미치는 진동들의 특성을 보여줍니다. 이 표를 통해서 대략 어떤 주파수 영역대의 진동이 자동차에 전달되는지 알수있고, 검은 동그라미는 자동차에 영향을 높게주는 변수들을 의미합니다. 자동차의 진동을 시물레이션 하기위해서 자동차를 하나의 시스템으로 생각할 수 있습니다. 이때 이 시스템은 자동차의 운동방정식을 이용한 진동모델입니다. 예를 들면, 입력값으로 울퉁불퉁한 노면의 높이, 자동차의 속도 등을 정하면, 이 시스템은 입력값에 대한 출력값으로 물리적 값인 가속도, 힘, 진동 변위 등을 알 수 있습니다. 이를 평가하여, 자동차의 안람함, 안정성, 내구성 등을 평가할 수 있습니다. 

위 그림은 다양한 도로의 불균일성과 자동차의 기능 요구 사항에 대한 감쇠의 평가 기준을 보여줍니다. 승차감은 전체 주파수 범위(영역 1)와 매우 낮은 진동 변위에서 영향을 받습니다. 차축과 차체의 움직임은 특정 고유 진동수에서 확인될수 있습니다(2, 4). 차축의 역위상 진동(3)은 일반적으로 차량의 다른 진동 시스템과의 상호 작용에서 발생합니다. 낮은 감쇠 및 짧은 스트로크의 감쇠의 경우, 소음으로 인해 부정적으로 보여지는 작동(기계적 구조적 스트로크 제한, 5)은 감쇠 값이 높거나 스트로크 크기에 민감한 감쇠를 사용하여 방지합니다. 

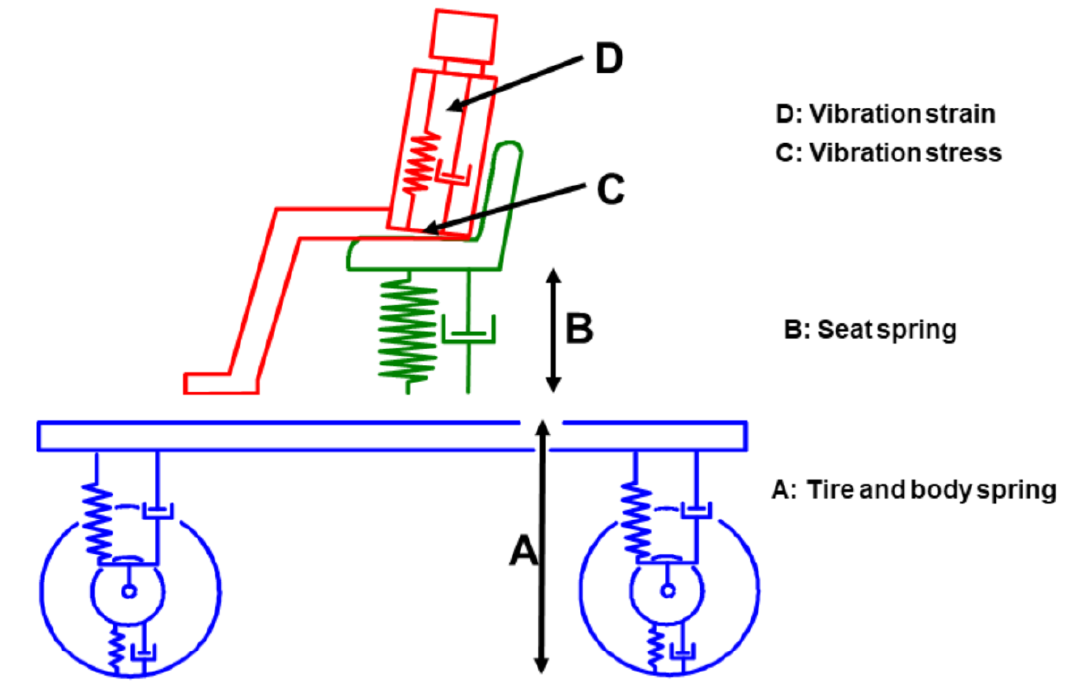
주행 편의성에 있어서 z방향의 신체 가속도는 가능한 한 작아야 한다는 요구 사항에 덧붙여, 진동 가속도는 운전자의 편안함 정도를 측정하기 위해 평가됩니다. 여기서, 타이어 스프링을 통해서만 튀어오르는 차량(예: 작업/건설 기계)은 특히 높은 주파수에서 편의성 성능평가가 매우 저조합니다. 운전자가 과도한 가속도에 노출되지 않도록 하기 위해 이러한 차량에서는 별도로 강성과 감쇠감이 있는 시트가 특히 중요합니다. 차량의 진동 시스템 마지막에는 운전자가 앉아있는데, 운전자의 신체 또한 진동합니다. 전체 차량 시트 및 운전자 진동 시스템은 위 그림에서 확인할 수 있습니다. 타이어와 차체 서스펜션(A) 및 시트 서스펜션(B)을 통해 시트 표면을 통해 자극을 받습니다. 인체 공학은 사람에게 영향을 미치는 진동 스트레스(C)와 이러한 스트레스가 신체에서 유발하는 진동 스트레스(D)를 구분합니다.

그림의 상단은 시험자가 앉아 있는 테이블의 진동에 대한 수직 방향의 머리와 어깨 진동의 진폭을 나타낸 것입니다. 사람의 머리와 어깨는 약 4Hz 범위에서 특정 공명 현상이 일어납니다. 약 6Hz 이상의 주파수에서는 피실험자의 진동은 낮게 유지됩니다. 따라서 인체는 이 주파수 영역에서 감쇠기 역할을 합니다. 그림의 아래 부분은 머리와 어깨의 가속도를 비교합니다. 약 30Hz 범위에서 머리의 가속도가 강하게 증가합니다. 운전자의 주행 편의성을 높이기 위해서 이러한 주파수 영역에 도달하지 않도록 해야 합니다. 따라서 우리는 이러한 주파수와 진폭 등을 평가할 필요가 있습니다. 일반적으로 알려진 주파수 평가는 두가지 역할을 합니다. 첫번째로 사람에게 미치는 기계적 진동 주파수에 가중치를 줄 수 있습니다. 위에서 언급했듯이, 우리 신체는 영역마다 공진주파수가 다르기 때문에, 이러한 가중치를 통해서 운전자의 주파수와 진폭의 관계를 평가할 수 있습니다. 그 뿐만 아니라 여러 가지의 주파수의 폭을 제한하기도 합니다. 주파수 가중치와 관련 주파수 범위는 응력 기준, 진동 도입 지점 및 진동 방향에 따라 달라지므로 다양한 평가방법을 정의할 필요가 있습니다.

휠 하중 F_Z, w은 차량 진동에 대한 첫 번째 평가 기준으로 간주되고, 주행 안전 및 도로 불균형을 평가할 수 있습니다. F_Z, W는 정적 부분과 동적 부분으로 구성됩니다. 차량 중량이 일정할 때 동적 휠 하중 성분의 일반적인 평균값은 0입니다. 휠 하중의 동적 부분은 위에 표시된 것처럼 양수 또는 음수일 수 있습니다. 따라서 휠 하중 변동의 표준 편차의 제곱은 휠 하중의 분산을 효율적으로 나타낼 수 있습니다. 특수한 경우 F_Z, W, dyn = -F Z, W, stat의 경우 총 휠 하중은 0이 됩니다. 이때 휠은 휠 접촉력 부족으로 인해 종방향 또는 횡방향 힘을 전달할 수 없습니다. 이 상황에서 휠은 제동이나 조향 조작에 기여할 수 없습니다. 또한 각각 휠 하중의 갑작스러운 손실은 불안정한 주행 조건으로 이어질 수 있습니다. 따라서 일반적으로 높은 주행안정성에서는 휠 하중의 변동이 매우 작습니다. 표준편차의 절대 크기는 기존의 정적 휠 하중 F_Z, W, stat에 따라 다른 영향을 미칩니다. 예를 들어 F_Z, W, stat = 20000 N인 트럭의 표준 편차 1000 N은 주행 안전에 거의 영향을 미치지 않지만 휠 하중이 3000 N에 불과한 자동차의 경우에는 매우 큰 영향을 미칩니다. 이를 고려하면서 주행 안전성을 평가하기 위해 동적 휠 하중을 정적 휠 하중과 연관시켜 평가하고, σ_F / F_Z, W, stat값은 가능한 한 작아야 합니다.

위 그림은 z방향으로 움직이는 질량 m에 대한 진동 시스템입니다. 여기서 바퀴는 질량 없고, 울퉁불퉁한 노면을 지나간다고 가정을 해봅시다. z=0은 정적 정지 상태입니다. (이미 위의 질량m 은 z방향으로 중력을 받음, 따라서 스프링이 이미 조금 줄어든 상태라고 가정). 이때의 운동 방정식은 다음과 같이 정리할 수 있습니다.

이때 스프링에 작용하는 힘은 상대적인 움직임을 고려해 다음과 같이 정리할 수 있습니다. 감쇠힘 또한 같은 방법으로 정의될 수 있습니다.

여기에서 c는 용수철상수, d는 감쇠상수입니다. 이 상수들은 선형이며, 이는 위에 그림을 통해 확인할 수 있습니다. 따라서 이 시스템은 선형시스템이고, 이 시스템은 2차 미분방정식을 통해 다음과 같이 나타낼 수 있습니다.

이 미분방정식의 우항에는 일명 “강제함수”가 위치하는데, 이들은 시스템에 진동을 일으키는 외부의 힘을 의미합니다. 따라서 시스템의 입력값이라고 생각할 수 있습니다. 이러한 비제차 미분방정식의 경우는 제차해와 특수해를 따로 계산한 뒤, 합하여 일반해를 찾을 수 있습니다. 즉, 우항에 0을 대입하고 제차해를 찾아 줍니다. 이때의 운동방정식은 관성력, 감쇠력 그리고 탄성력의 합이 0임을 나타냅니다.

위 그림은 감쇠 강제진동의 한 예를 보여줍니다. 감쇠력(D)에 의해 진동이 시간이 감에 따라 어떻게 줄어드는지 알 수 있습니다. 특수해를 구할 때 주로 조화함수 h(t)를 많이 이용합니다.

 조화함수를 미분하고 운동방정식에 대입해 특수해를 찾아줍니다.

자동차를 이러한 진동시스템이라 가정하면, 자동차에 발생하는 진동은 외부의 강제진동에 굉장히 민감하게 변합니다. 위의 그림은 ω, v, L 사이의 관계를 이중 로그 그래프로 나타낸 것입니다. 여기에는 자동차에서 일반적으로 발생하는 본체, 좌석 및 바퀴의 고유 진동수를 알 수 있습니다. 자동차에 대한 이 3가지 고유진동수의 범위는 0.7~15Hz이며, 36~180km/h의 속도 범위에서 주파수 하한이 0.5Hz, 상한 30Hz인 경우 L = 0.3~100m의 파장 자동차의 수직방향 동역학이 중요합니다. 지금까지 파장의 이상적인 경우를 생각해 보았지만 실제로는 전혀 그렇지 않습니다. 실제 도로를 설명할 때 주기적인 노면충돌과 확률적(불규칙한) 노면충돌을 구분합니다. 주기적인 노면충돌은 파장이 다른 여러 정현파 진동을 합산하여 푸리에 급수를 사용하여 설명할 수 있습니다. 이때 진폭비가 다른 여러 외부주파수가 동시에 차량 시스템에 작용합니다. 진동시스템에 영향을 미치는 확률적 노면충돌은 통계적 방법을 사용하여 설명될 수 있습니다. 예를 들면, 장기간의 평균 제곱근 값과 표준 편차 또는 산포도를 통해서 설명될 수 있습니다.

위 그림은 각각의 진동시스템에서의 변수들이다. 휠 하중 변화 및 차체 가속도의 변화에 대한 개별 매개변수의 영향은 시뮬레이션 계산을 통해 알 수 있습니다. 이때 바디 스프링 강성 c_B, 차체 질량 m_B, 차체 감쇠 d_B, 타이어 스프링 강성 c_W 및 타이어 스프링 질량 m_W 등 변수에 변화를 주면서 진동 시스템에 미치는 영향을 비교할 수 있습니다. 자동차의 수직역학을 검사하기 위해서 ¼ 차량모델이 이용될 수 있습니다. 이 모델은 차체의 이동 변위z_b, 휠의 이동 변위z_w라는 2차 자유도 모델입니다. 노면 충돌로 부터 올라오는 외부충격은 z_0을 나타냅니다. 이뿐만 아니라 차체의 질량, 휠의 질량 또한 분배됩니다. 위 시스템은 위 그림에 나온것처럼 운동방정식을 정리할 수 있습니다.

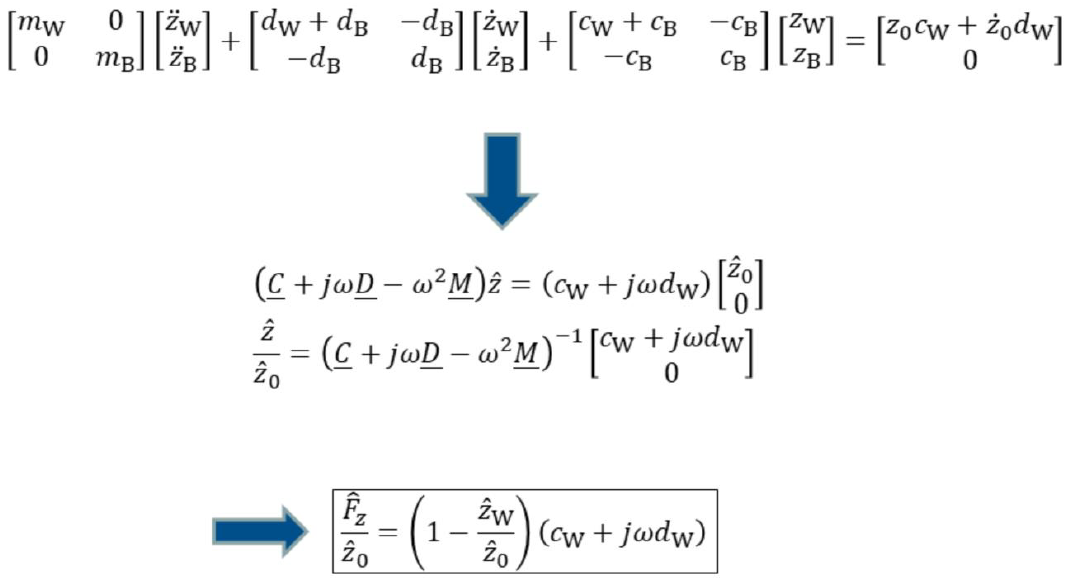
감쇠를 무시하면 고유값을 계산해야하고, 행렬식을 계산하여 시스템의 고유 주파수를 결정할 수 있습니다. 이러한 계산과정은 위에서 알 수 있습니다.

위 그림은 질량의 진동응답에 대한 영향을 보여줍니다. 체중 m_B는 229kg에서 246kg으로, 335kg에서 391kg으로 변경되었으며 다른 변수는 변경되지 않았습니다. 진폭비를 보면 차체 질량 증가는 차체 가속도에 긍정적인 영향을 미치는 것을 알 수 있습니다. 그 이유는 질량이 증가하면서, 관성이 증가하기 때문입니다. 반면에 차체의 질량 증가는 동적 휠 하중에 미미한 영향을 미칩니다. 질량 증가에 따른 힘의 증가는 가속도 감소로 상쇄되기 때문입니다.

차체 스프링 강성 c_B 또는 차체 질량 m_B의 변화는 차체의 고유 진동수 f_e의 변화에 영향을 줍니다.

스프링 강성 c가 증가함에 따라 고유 진동수 f_e는 점진적으로 증가하고 질량(하중, m_load> 0)이 증가함에 따라 그에 따라 감소하는 것으로부터 알 수 있습니다. 위 그림은 차체 강성(화살표 방향)이 증가하는 차량에 대해 서로 다른 강성의 결과를 통해 차체 고유 진동수의 변화를 보여줍니다. 바디 강성 c_B의 스프링 강성은 5.1kN/mm에서 10.1kN/mm로, 20kN/mm에서 40.4kN/mm로 증가했습니다. 스프링 강성 또는 차체 고유진동수가 증가함에 따라 차체 가속도의 진폭비가 모든 영역에서 증가하는 반면 휠 하중 진폭비는 초기에 증가하고 휠 하중 공진 범위에서는 감소함을 알 수 있습니다. 즉, 단단한 서스펜션의 경우 공진 지점이 더 높은 진동수(더 높은 고유 진동수)로 이동합니다.

위 그림은 진폭비의 차체 감쇠 d_B의 영향을 보여줍니다. 여기서 감쇠 상수 d_B는 230Ns/m에서 680Ns/m, 1140Ns/m, 1600Ns/m에서 2050Ns/m로 증가했습니다. 감쇠 상수 D가 0.05에서 0.45로 증가했습니다. 차체의 고유 진동수(f_e = 14Hz)를 포함한 다른 모든 변수는 일정하게 유지되었습니다. 차체 가속도와 차륜 하중 변동의 공진 범위에서 감쇠가 증가함에 따라 진폭비가 감소함을 알 수 있습니다. 반면에 더 높은 진동수에서는 감쇠가 증가함에 따라 휠 하중 진폭비 변동이 감소하는 것이 눈에 띕니다. 그러나 차체 가속도 진폭비는 급격히 증가하여 운전자의 편안함이 감소합니다. 더 강력하고 속도에 따라 달라지는 댐퍼 힘이 휠 하중 변동을 상쇄하지만 동시에 시스템에 추가적인 힘이 발생되기 때문에 차체에 더 높은 가속도로 이어집니다.

지금까지의 결과를 요약하면 스프링 강성과 댐핑을 조정할 때 주행 편의성(차체 가속도)과 주행 안전성(관련 휠 하중 변동) 측면에서 절충안을 찾아야 한다는 것을 알 수 있습니다. 두 기준을 그래픽으로 표시하면 좋은 평가곡선를 볼 수 있습니다. 가변 댐핑과 그 반대의 일정한 바디 스프링 강성의 선이 그림에 나와 있습니다. 그림에 따르면, 가장 작은 K 값과 동시에 낮은 σ_F / F_Z, W, stat 값이 이 그래프의 한계 곡선을 나타냅니다. 이 물리적으로 결정된 한계 곡선은 차체 편안함과 운전 안전성을 위해 반대 방향으로 진행됩니다. 이는 휠 하중 변동과 차체 가속도의 진폭 수준을 동시에 최소화할 수 없음을 의미합니다. 이 다이어그램은 "충돌 다이어그램"이라고도 합니다.

휠 질량의 영향은 24kg에서 31kg, 62kg으로 증가시키며 측정되었습니다. 휠 질량에 영향을 미치는 설계는 단단한 차륜으로부터 독립적인 휠 서스펜션으로 전환하거나 브레이크를 휠에서 안쪽 차륜쪽으로 재배치하는 것입니다. 오늘날 고급 차량에 쓰이는 McPherson 서스펜션의 무게는 약 40~45kg입니다. 휠 질량을 줄임으로써 휠의 고유 진동수가 증가합니다. 이 그림은 또한 휠 질량의 영향이 주로 휠 공진 범위(8~14Hz)에서 두드러짐을 보여줍니다. 따라서 휠 질량은 높은 진동수의 가진에 중요합니다. 휠 질량이 커지면 휠 공진 범위의 휠 부하 변동이 증가하고 진동수 스펙트럼이 넓어집니다.

휠의 고유 진동수에 영향을 미치는 또 다른 매개변수는 타이어 스프링 강성입니다. 이 예에서는 93.9N/mm에서 127.9N/mm를 거쳐 187.7N/mm로 변경되었습니다. 이 순서대로 9.65Hz에서 11.0Hz, 13.0Hz로 고유 주파수 f_e, W의 증가에 해당합니다. 더 높은 진동수 가진(강한 노면충돌)의 경우 큰 타이어 스프링 강성 c_W는 차체 가속도 및 휠 부하 변동과 관련하여 좋지 않은 영향을 미칩니다. 따라서 타이어의 수직 유연성을 무시해서는 안 됩니다. 자동차 기술 분야의 측정에 따르면 오늘날 자동차 타이어의 정적 타이어 스프링 강성(고정 휠)은 유형, 크기 및 타이어 내부 압력에 따라 c_W = 100 ~ 300 N/mm입니다. 타이어의 감쇠는 너무 낮아서 자동차에서 무시될 수 있으며, 자동차의 움직임은 주로 서스펜션에 의해 감쇠됩니다. 타이어 스프링 강성과 타이어 질량의 변화는 낮은 진동수 가진의 경우 별로 중요하지 않습니다.

차량 A는 특정 가진(주행 속도) 진동수부터 휠 하중이 급격하게 증가하고, 그로 인해 더 이상 운전할 수 없는 상태의 완전히 스프링이 없는 차량입니다. 차량 B는 차체의 경우 스프링과 감쇠 구조를 가지고 있지만 바퀴의 경우는 질량만 있는 상태입니다. 이 시스템의 구조는 두 질량 발진기인데, 2차 고유진동수가 무한히 높기 때문에 차량을 더 이상 특정 속도 이상으로 주행할 수 없습니다. 차량 C는 차체에 스프링 강성이 없는 차량에 해당합니다. 여기서 차량은 댐핑은 거의 없고 특정 스프링 강성효과가 있는 타이어를 사용합니다. 연결된 질량으로 인해 이 진동 시스템은 고유 진동수 영역에서 높은 동적 휠 하중을 발생시키고 따라서 이 영역에서 중요한 동작을 나타내는 단일 질량 시스템입니다. 차량은 여전히 ​​일반적으로 운전이 가능함을 알 수 있습니다. 트랙터 및 기타 상업용 기계가 이 차량에 해당합니다. 공기압 타이어의 발명은 차량 D가 증명하듯이 처음부터 고속 주행을 가능하게 했습니다. 타이어 스프링 단독 차량 C를 사용하면 더 높은 가진의 경우 바퀴 하중 변동이 이미 제한되지만 모든 가진 영역에서 바퀴 하중 변동을 제한할 수 있었던 것은 두 번째 질량과 강력한 감쇠 가능성을 통해서만 가능합니다.

2질량 발진기의 기본 고려 사항은 고르지 않은 노면에서 차량의 진동 거동에 대한 대략적이지만 유용한 추정치를 제공합니다. 그림은 탄성적으로 장착된 추가 질량(예: 시트에 드라이버, 진동 흡수 장치, 장착된 모터 등)이 추가될 때 진동이 어떻게 변하는지를 보여줍니다. 위 그림에서 진동 등가 시스템("3질량 진동자")은 일정한 감쇠 d_3로 강성 c_3을 증가시키기 위한 (좌석)가속도의 진폭비가 표시됩니다. 추가 질량 m_3의 세 번째 고유 진동수 f_e, 3에서 발생하는 세 번째 최대값을 볼 수 있습니다. 2N/mm에서 7.10에서 17N/mm로 시트 스프링 강성의 변화는 고유 시트 주파수 f_e, 3이 1.5Hz에서 2.5Hz로 또는 3.0Hz에서 4.0Hz로 증가한다는 것을 의미합니다. 공명 영역. 105Ns/m에서 264Ns/m로 시트 댐핑 d_3의 증가는 0.1에서 0.25에서 0.3의 시트 댐핑 정도 D_3에 해당합니다. 2질량 발진기와 마찬가지로 댐핑은 공진 범위에서 발생하는 진폭을 제한하는 데 특히 중요합니다.

이 그림은 앞 그림의 3질량 발진기로 엔진 질량(엔진 + 클러치 + 기어박스 + 전륜구동의 액슬 구동)을 시뮬레이션할 때 차체 가속도의 확대 기능을 보여줍니다. 점선은 견고한 엔진 마운트를 사용한 차체 가속도의 진폭비입니다. 낮은 감쇠(D_3 = 0.1, 실선)만 있는 탄성의 경우 강한 공진 증가 외에 12Hz에서 고유 엔진진동수 f_3는 최소값입니다.

차륜과 도로 사이의 수직하중 F_Z, W는 일정하지 않고 시간에 따라 변합니다. 동적 휠 하중 성분 F_Z, W, dyn은 수직 방향의 총 휠 하중이 0이 될 정도로 음수일 수 있습니다. 그러면 타이어와 도로 사이에 원주 방향 및 횡력 F_X, W 및 F_Y, W가 전달되지 않아 위험한 운전 조건으로 이어질 수 있습니다. 따라서 휠 하중 변동은 "안전운전"의 기준이 됩니다. 반면에 정적 휠 하중 F_Z, W, stat과 같은 방향으로 작용하는 차륜 하중의 변화는 도로에 추가적인 응력을 가합니다(상용 차량 서스펜션의 도로 친화적인 설계를 통한 도로 하중 감소). 따라서 주행 테스트의 일부로 여러 다른 측정 변수를 기록하는 것 외에도 동적 휠 하중을 결정해야 하는 경우가 많습니다. 이를 수행하는 한 가지 방법은 도로에 침몰된 휠 하중 눈금을 사용하여 z 방향으로 타이어와 도로 사이의 접촉 영역에 작용하는 힘을 측정하는 것입니다. 이 변형의 한 가지 장점은 찾는 휠 하중이 타이어 접촉 영역의 작동 위치에서 정확하게 기록될 수 있다는 것입니다. 단점은 측정 범위가 스케일 길이(일반적인 길이 약 0.5m)로 축소된다는 것입니다.

 

다성분 힘 측정 림은 타이어에서 림으로 전달되는 모든 힘과 모멘트를 기록할 수 있습니다. 타이어 질량을 가속하는 힘은 기록되지 않으므로 휠의 고유 진동수 영역에서 휠 하중을 결정하는 오류가 상당합니다. 그렇지 않으면 휠 하중 외에도 제동 또는 구동 토크 및 횡력과 같은 중요한 변수가 결정될 수 있습니다. 측정 림의 단점은 높은 진동 신호가 전송되지 않는다는 것입니다. 그림은 힘 측정 림의 기본 구조를 보여줍니다. 힘은 휠 접점에서 작용하고 타이어를 통해 분할 림으로 전달됩니다. 이것은 차량별 어댑터를 통해 힘을 실제 측정 요소로 전달하며, 여기서 축 방향 및 반경 방향 굽힘 빔의 힘은 탄성 변형을 일으킵니다. 이러한 변형을 기반으로 원래 도입된 힘에 대한 결론을 도출할 수 있습니다. 림은 테스트 차량의 휠 캐리어에 나사로 고정된 소위 허브 어댑터를 사용하여 차량에 부착됩니다.

 

출저: Ride and Handling, Automotive engineering in Darmstadt, TU Darmstadt, Germany